Гравилет. Задача 4-х точек
С проблемой гравилета все ясно на основе решения "Задачи 4-х точек".
Нет сомнений в том, что после Второй Мировой Войны оказался востребованным далеко не весь уникальный научно-технический потенциал поверженной Германии.
Примерно так же был разбазарен и наш научно-технический потенциал после поражения в Холодной войне.
И во многом подобные вещи случаются по причине наличия таких экспертов, которые, будучи очарованными одними научно-техническими достижениями, чрезвычайно много усилий тратят именно на объяснение причин невозможности использования других... Как это и случилось, быстрее всего, с тем же инерциоидом, который по некоторым данным, был все же испытан немцами в 1944 году (см.: evg-ars.narod.ru/Eng.htm ).
Начало обсуждения темы гравилётов - здесь: www.coza.ru/article/theme/problema_gravileta_okon4atelno_re6ena.htm
По мотивам статьи «СТАНЦИЯ В ТОЧКЕ ЛИБРАЦИИ»
А. БРЫКОВА, заслуженного деятеля науки
и техники РСФСР, лауреата Ленинской
премии, доктора технических наук,
профессора,
опубликованной в журнале "Авиация и космонавтика" 1987 № 7. С. 42-43
«В опубликованных на страницах журнала статьях неоднократно приводились факты, убедительно свидетельствующие о том, как космонавтика активно содействует развитию науки, техники, народного хозяйства, ускоряет технический прогресс. Бесспорно, она имеет большое будущее. Сегодня даже трудно представить всю совокупность технических и народнохозяйственных проблем, которые будут решены с использованием космических средств. О некоторых возможностях космонавтики будущего, в частности об использовании космического пространства в районе точек либрации системы Земля – Луна, и пойдет здесь речь.
В теории понятие о точках либрации возникло давно. Закон всемирного тяготения, открытый Ньютоном, дал возможность ученым предсказывать движение планет. Однако попытка с требуемой точностью спрогнозировать движение Луны не увенчалась успехом. Дело в том, что на движение естественного спутника нашей планеты помимо Земли существенно влияет Солнце».
Дело в том, что, в действительности, окружающий нас мир состоит из одних только незамкнутых систем (НС) даже если не принимать в расчет влияние на них Солнца.
Дело еще и в том, что почти все происходящие вокруг нас взаимодействия, так или иначе, заканчиваются воздействием на самую большую массу из нашего окружения, а именно на Землю.
Так, в частности, и мы сами при ходьбе или беге воздействуем именно на нее. На нее, в конечном итоге, оказывает воздействие и самолет летящий на большой высоте (через соответствующий скос потока) и ракета, выводящая спутник в космическое пространство, т.к. частицы ее реактивной струи почти во всех случаях остаются микроспутниками той же Земли, соответствующим образом воздействуя и на нее.
«Так перед учеными возникла проблема решения задачи трех тел: Солнце – Земля – Луна. Заметим, что в конечном аналитическом виде она не решена и по настоящее время. Лишь несколько частных случаев нашли Эйлер и Лагранж.
Исследования Эйлера и Лагранжа, долгое время рассматриваемые лишь как красивые теоретические построения, в наши дни приобрели большую практическую значимость. Многие автоматические межпланетные станции движутся в гравитационном поле Земли и Луны. В этих случаях мы имеем дело с ограниченной задачей трех тел. Как показали Эйлер и Лагранж, частные ее решения определяют координаты пяти точек, обладающих уникальными свойствами. Они и получили название либрационных (или просто точки либрации). Чем же они замечательны? Космическая станция (материальная точка с пренебрежимо малой массой по сравнению с Землей и Луной), находящаяся в окрестности точки либрации, будет там вечно двигаться, соблюдая вполне определенное, не изменяющееся во времени положение относительно двух притягивающих центров. А это значит, что упрощается процесс управления движением космического аппарата, сокращается объем навигационной измерительной информации» и т.д.
Но, как стало ясным еще в 1963г., когда появилась схема так называемых безрасходных межорбитальных переходах пульсирующей космической гантели, речь можно вести и о вполне определенной ясности с «ограниченной задачей четырех тел», причем, имея в виду значительно более масштабные перспективы ее практического использования, причем, именно на Земле.
При этом речь идет о том, что вместо «материальной точки с пренебрежительно малой массой по сравнению» с двумя «притягивающими центрами» в этом случае используется гантель, образованной, соответственно двумя материальными точками. Естественно, при этом их массы являются также пренебрежительно малыми.
И прежде всего эти перспективы связаны с возможность организации в этом случае и взаимное отталкивание таких «притягивающих центров», как те же Земля и Луна, что на практике вполне может нами восприниматься и как проявление такого эффекта, как и тот, при помощи которого, быстрее всего, немцы сумели в 40-х годах ХХ столетия осуществить безопорные полеты своих «летающих тарелок» (рис. 1).
Суть же безрасходных межорбитальных переходов в данном случае сводится к тому, что их может осуществить обычный спутник 1 (рис. 2), если его разделить на две половинки 2.
За счет же организации периодического расталкивания этих половинок на расстояние 3 по нормали к плоскости орбиты центра масс (ц.м.) гантели этот ц.м. в качестве мнимой точки начинает раскручиваться по спиралеобразной (многовитковой) орбите. В конечном итоге, все это (при достаточно длительном времени совершения половинками гантелей своих колебаний) оборачивается смещением ц.м. гантели и той же Земли во взаимно противоположные стороны, как при обычном реактивном расталкивании масс.
При однократном же мгновенном разлете половинок на достаточно большое расстояние друг от друга ц.м. гантели может сразу же перейти с эллиптической орбиты, например, на гиперболическую.
Что касается Земли, то она в подобных случаях совершает точно такие же межорбитальные переходы, но, естественно, без разделения ее на половинки.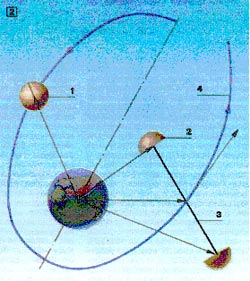
В принципе, точно такие безрасходные межорбитальные переходы гантели можно организовать и вокруг выше упомянутых точек либрации, со свойствами которых нам проще всего разобраться на примере системы Земля – Луна.
Соответствующие «точки либрации L1 – L5 располагаются в плоскости орбиты Луны (рис. 3). Три из них, называемые коллинеарными, находятся на прямой, проходящей через центры масс Земли и Луны. Первая расположена между Землей и Луной. Если расстояние между Землей и Луной на какой-либо момент обозначить через r, то удаление первой точки от Земли всегда характеризуется расстоянием, равным ~ 0,849 r. Вторая располагается за Луной на расстоянии от нее ~ 0,169 r. Третья находится по другую сторону Земли и удалена от нее на ~ 0.992 r. Четвертая и пятая расположены так, что в плоскости орбиты Луны образуется ромб со сторонами, равными r, в вершинах которого находятся Земля, L4, Луна и L5, или два равносторонних треугольника. Поэтому их называют треугольными точками либрации.

Рис. 3 (слева). Расположение точек либрации в системе Земля – Луна.
Примечательно, что все точки либрации строго соблюдают свое вполне определенное положение в системе Земля – Луна. И еще одно удивительное свойство: в идеальном случае помещенная с небольшими начальными возмущениями в такую точку космическая станция будет длительное время совершать вблизи нее колебательные движения (отсюда название «либрационные»)».
В принципе, нас интересует случай наличия у Луны нулевой орбитальной скорости, а значит ее падения на Землю, соответственно, вместе с первой точкой (L1).
При этом является очевидным, в частности, и то, что безрасходные межорбитальные переходы гантели можно осуществлять еще и одновременно вокруг точки L1 и Луны.
Тем не менее, заменив для упрощения все участвующие в рассматриваемом взаимодействии тела материальными точками, мы можем сделать ряд вполне определенных выводов.
Во-первых, это касается того, что увеличение массы (m), находящейся в точке L1, однозначно ведет к дополнительному подтягиванию друг к другу Земли и Луны.
Во-вторых, если организовать наличие у Луны и массы m, например, взаимно противоположных и достаточно мощных электростатических зарядов, то на характер движения точки L1 можно влиять и соответствующим увеличением интенсивности этих зарядов. За счет этого можно организовать и хотя бы временное неподвижное положение этой точки. В этом случае, правда, она будет выступать уже в качестве своего рода комплексной точки L1*.
В-третьих, такого рода изменение характера движения точки L1* сопровождалось бы ускорением падения на Землю самой Луны.
В-четвертых, на характер движения точки L1 можно также воздействовать и путем организации вокруг ее все тех же безрасходных межорбитальных переходов гантели, что, в принципе, эквивалентно, обычному реактивному расталкиванию ее и также мнимой точки L1, образованной такими «притягивающими центрами», как Земля и падающая на нее Луна.
При этом очевидным является и то, что в данном случае реактивное расталкивание периодически пульсирующей гантели и мнимой точки L1 на самом деле сводится к расталкиванию ее одновременно именно с теми массами, которые эту точку L1 и образуют, т.е. с Землей и Луной. Такого рода взаимодействие, фактически, 4-х масс вполне может рассматриваться наблюдателем, находящимся на поверхности Земли, и как вполне определенное проявление гравилетного эффекта.
Как раз такого рода реактивным расталкиванием Земли и падающего на него тела (вместе с аналогом пульсирующей гантели, вращающейся вокруг точки L1) для организации соответствующего безопорного полета, быстрее всего, в свое время и воспользовались немцы.
Действительно, вот чем характеризуется, в частности, обычное реактивное расталкивание массы m с точкой 1, образуемой, как уже отмечалось, такими «притягивающими центрами», как Земля (масса Mзмл) и такой аналог Луны, как обычное атомное ядро (масса Мая).
Соответствующее дистанционное взаимодействие четырех масс в этом случае не так уж и сложно описать системой из следующих 3-х уравнений:
1. m = m1 + m2;
2. m * dVm = Mзмл * dVзмл + Мая * dVая;
Jгр = Mзмл * dVзмл = m * dVm + Мая * dVая;
3. Е0 = Еm + Еая + dЕзмл;
2*Е0 = Jгр * dVзмл + m*[(Vm*Vm) – (Vm-dVm)*(Vm-dVm)] + (Jгр - m*dVm)*dVая;
2*Е0 = Jгр * (dVзмл + dVая) + m*dVm*(2*Vm - dVm - dVая);
где:
m1 и m2 – половинки гантели массой m;
Jгр – импульс рассматриваемого реактивного взаимодействия между массой m и точкой L1*.
Е0, Еm, Еая и Езмл – суммарная кинетическая энергия рассматриваемого реактивного взаимодействия и, соответственно, массы m, АЯ и Земли (при условии нахождения всех их первоначально в неподвижном положении, в частности, за счет вполне определенного начального расталкивания Земли и АЯ);
Vm, dVзмл, dVm и dVая – скорость массы m, приращения скоростей Земли, масс m и Mая (без представления об их направлениях) в результате осуществления рассматриваемого реактивного взаимодействия, имея в виду, что dV уменьшает скорость Vm.
С учетом же следующих очевидных неравенств:
dVзмл << dVая << Vm,
соответственно, в первом, но достаточно точном приближении (после корректного исключения заведомо меньших величин) получим:
2*Е0 = m*dVm*(2*Vm - dVm) + Jгр*dVая;
Jгр = [2*E0 - m*dVm*(2*Vm – dVm)]/dVая.;
Yгр = [2*E0 - m*Gm*(2*Vm – dVm)]/dVая.;
где:
Yгр = g*(m + Mая) – как бы гравитационная сила, компенсирующая воздействие сил земного притяжения (с ускорением g);
N0 – суммарная мощность, развиваемая в процессе рассматриваемого взаимодействия.
Gm – ускорение массы m (в направлении от Земли).
Таким образом, можно составить следующее равенство:
g*(m + Mая) = [N0 - m*Gm*(2*Vm – dVm)]/dVая,
что с учетом, в частности, приведенных ниже характеристик водородного летательного аппарата (ЛА), который, как это становится очевидным, вполне может быть изготовлен на практике (из стеклянных микросфер, наполненных водородом высокого давления) в качестве аналога атома гелия, обладающего способность проникать в космическое пространство, сводится к следующему неравенству:
10*(15 + 15000) > [2N0 - 15*10*(2*500000 - dVm)]/dVая;
150150*dVая > 2N0 - 150000000 + 150*dVm ;
N0 < 75000000 - 75*dVm + 75075*dVая [Вт],
где:
Vm > 500000 м/сек;
Mая/m = 1000.
Мая = 15000 кг.
Как является очевидным, при достаточно малых значениях dVm, соответственно, значительно больших dVая, что как раз и сводится к проявлению как бы гравилетного эффекта, потребное значение N0, оставаясь меньше 75000 КВт, почти не зависит от dVm и dVая, вне зависимости от их направлений.
Соответственно, получаем следующее соотношение:
Yгр/N0 < 150150/75000000 = 0.002 н/Вт,
что является вполне приемлемой величиной в сравнении, например, с воздушными пропеллерами, у которых соотношение тяги и мощности равно:
T/N0 = 40 н/л.с. = 0.054 н/Вт.
Нечто подобное, соответственно, происходит и при вращении той же гантели массой m вокруг точки либрации и массы Мая – из-за малого расстояния между ними.
Таким образом, используя «свойства первой коллинеарной точки либрации, можно» не только «в значительной мере сократить энергозатраты на проведение экспедиций на Луну», но и организовать безопорное движение в окрестностях Земли.
Более того, вполне можно утверждать и то, что соответствующее безопорное движение изначально существует в нашем окружении. Ведь только на такой основе можно объяснить факт самостоятельного проникновения в космическое пространство гелия, сопровождающееся еще и выводом в космическое пространство некой полезной нагрузки (ПН), имея в виду что в этом качестве выступает масса нейтронов, наличием которых тот же гелий, собственно, и отличается от водорода.
И в этом плане оболочка, наполненная водородом, и имеющая (вместе уже с обычной ПН) такую же массу, как и тот же водород, является, фактически, полным аналогом того же гелия, способного проникать в космическое пространство. При этом имеется в виду равенство масс водорода и тех же нейтронов.
И обусловлено все это не только тем, что земная атмосфера, но и космическое пространство на 99% наполнено именно наиболее легкими газами: водородом и гелием, соответственно, на 90% и 9% («Суперсила» П. Девиса, издательство «Мир», 1989, стр. 25), оставляя на долю других элементов, включая те же звезды и планеты, всего лишь 1%.
Хотя, все же следует подчеркнуть, что некоторыми исследователями приводятся и другие цифры, которые, тем не менее, сути проблемы не меняют.
Что же касается уже упомянутых стеклянных микросфер, то их, в принципе, не так уж и сложно изготовить.
Они уже давно используются в качестве, кстати, абсолютно безопасных, но, тем не менее, заведомо перетяжеленных мишеней при термоядерных исследованиях. Их-то, как и нанотрубки, по всей видимости, и можно было бы использовать, как некий пористый материал для изготовления ЛА, способного совершать безопорный полет, что так нравится авторам фантастических произведений.
Прислал: Акинин (за что огромная благодарность!).
